切屑堂 kirikuzudo
ブログ： 2020/09/20 ボルト締結体の検討（その３）
＜１．TLに流れてきた図＞
9月の初め頃に「やってはいけない設計？」みたいなTweetがTLに流れてきました。
下のような図を含んだTweetです。
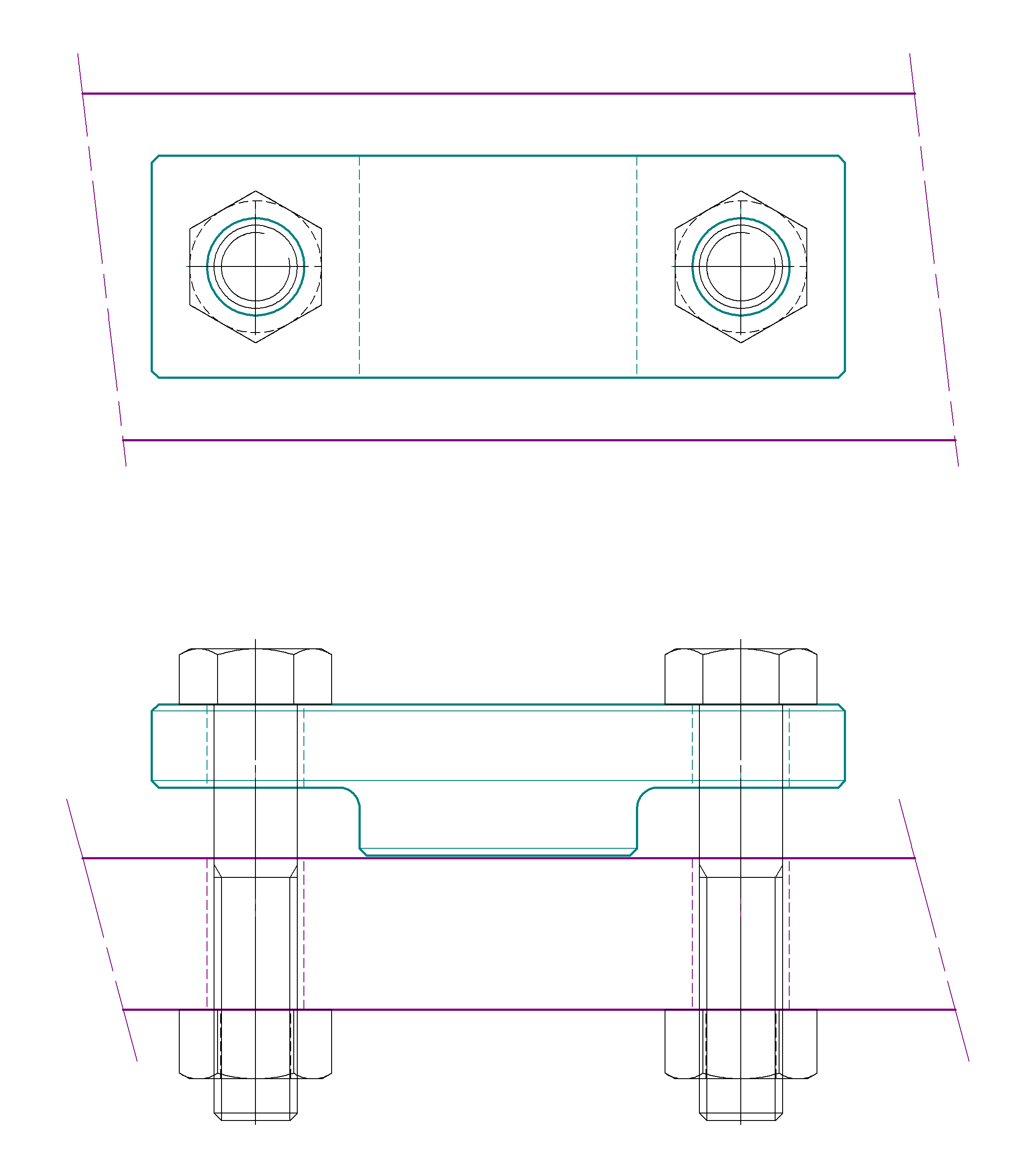これを見て自分がしたTweetが下記です。
---------
（「やってはいけない設計」みたいなのが流れてきたが、
管フランジ締結体を全否定されてる感じだし、
実際の寸法形状と使用環境・運用による、だと思いますね。
数字置いてみるまではわかんなやつ。
ただ計算めんどいので避けれるなら避けたほうがいい、
という話ならわかります。）
---------
で、Tweetした後に、これ単純に
「外力の作用位置と被締結物のばね定数」
の話だよなあ、となりまして。
つまり、ちょうどいい題材がやってきた感じですね。
＜２．おさらい＞
話をすすめる前にざっくりとボルト締結体の考え方のおさらいです。
・M5～M16ぐらいの機械構造用六角ボルトには標準的な締付け軸力がある。
・ボルト締結体に外力が作用した場合、
この外力はボルト軸力増加分と被締結物の圧縮(曲げ)変形分に按分される。
・外力の按分具合は内外力比という比率で決まる。
・被締結物の圧縮ばね定数とボルトの引張ばね定数で内外力比が決まる。
・内外力比は外力作用位置／軸力作用位置によって修正され、
ボルト軸から外力作用位置まで距離がある場合、
修正係数は0.15前後の低い値になることがある。
・修正係数は適用範囲が限られたいくつかの実験式があるだけで、
理論的あるいは定量的に求めることは難しい。
詳細は下の過去記事を参照してください。長くて読みにくいですけど。
「ボルト締結体の検討（その１）」
http://kirikuzudo.sblo.jp/article/187148956.html
「ボルト締結体の検討（その２）」
http://kirikuzudo.sblo.jp/article/187194450.html
「六角ポルトの強度区分について」
http://kirikuzudo.sblo.jp/article/187638425.html
＜３．数値解析で被締結物(上)の圧縮ばね定数を求める＞
今回は下の考え方を試してみます。
・修正係数を用いずに被締結物の見かけの圧縮ばね定数を、
数値解析(Nastran等のFEM)を用いて求めることで
実用的な内外力比を得られる(要検証)
TLに流れてきた図のような複雑な形状について、
修正係数を理論的に求めるのは難しいと思います。
そして、そもそもなぜ修正係数が必要かというかと、ざっくりした言い方をすれば、
「外力作用位置や軸力作用位置によって
被締結物の見かけの圧縮ばね定数が変化するから」
です。
逆に考えれば、変化した被締結物の見かけの圧縮ばね定数がわかるのであれば修正係数を使わないで済ますことができます。
そこで、数値解析でボルト軸力および外力を荷重としてかけたときのＺ方向最大変位をもとに、被締結物の見かけの圧縮ばね定数を求め、これを使って内力係数を決定することにします。
TLに流れてきた図は具体的な寸法が入っていなかったので、下図のように寸法を決めておきます。ボルトはM12 x 60Lです。
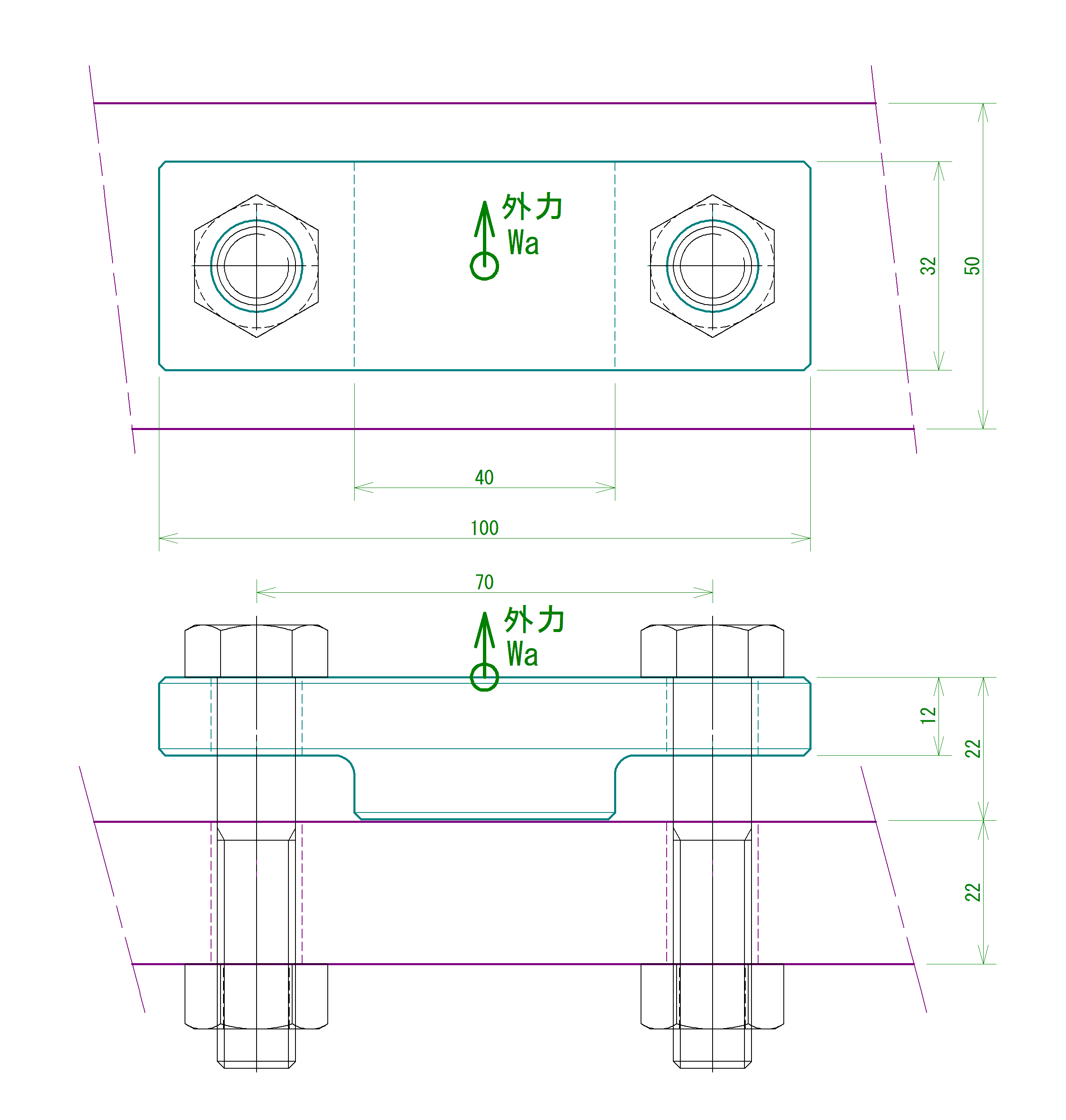これを元にAutodesk InventorでNastran用のモデルを作ります。
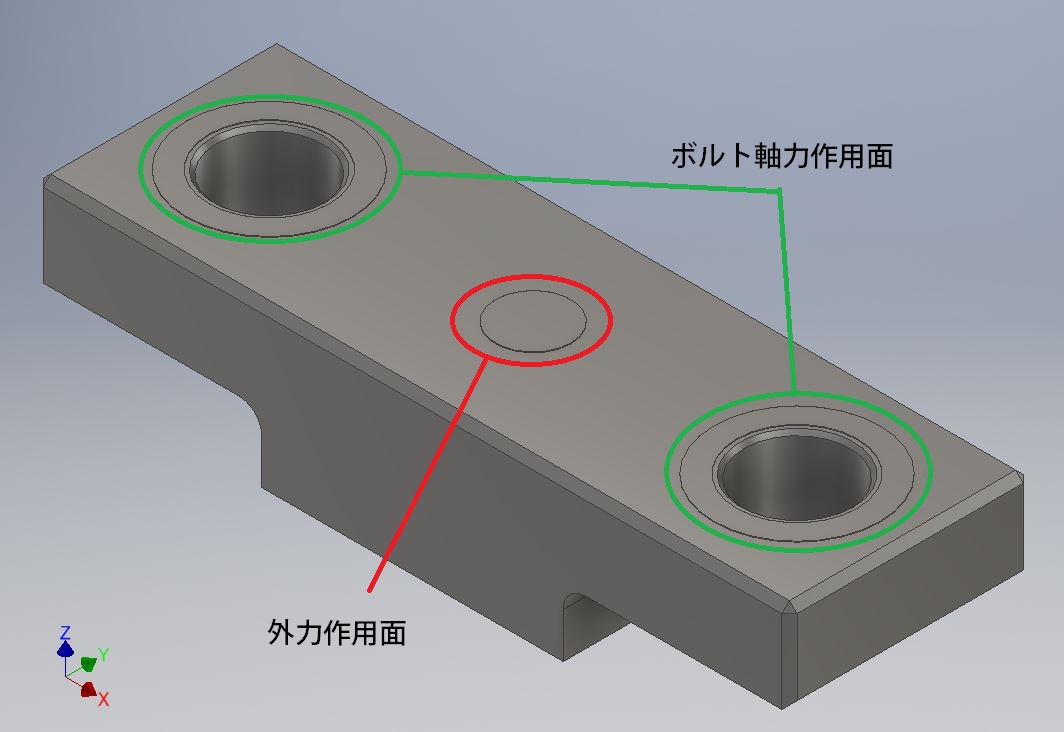※フィレット半径はFEMかけながらフォンミーゼス応力を見て6[mm]にしました。
Nastranで次の条件を入れて線形静解析をかけます。
・メッシュ設定はParabolic 2[mm]
・荷重はボルトの座の部分で受けます
・T字の底面を固定拘束
・荷重はM12のT系列標準軸力17500[N]
・外力はＺ(+)方向に5000[N]
＜４．Autodesk Nastranでの線形静解析の結果＞
結果は以下になります。
↑フォンミーゼス応力でフィレット部が424[MPa]にいってますね。
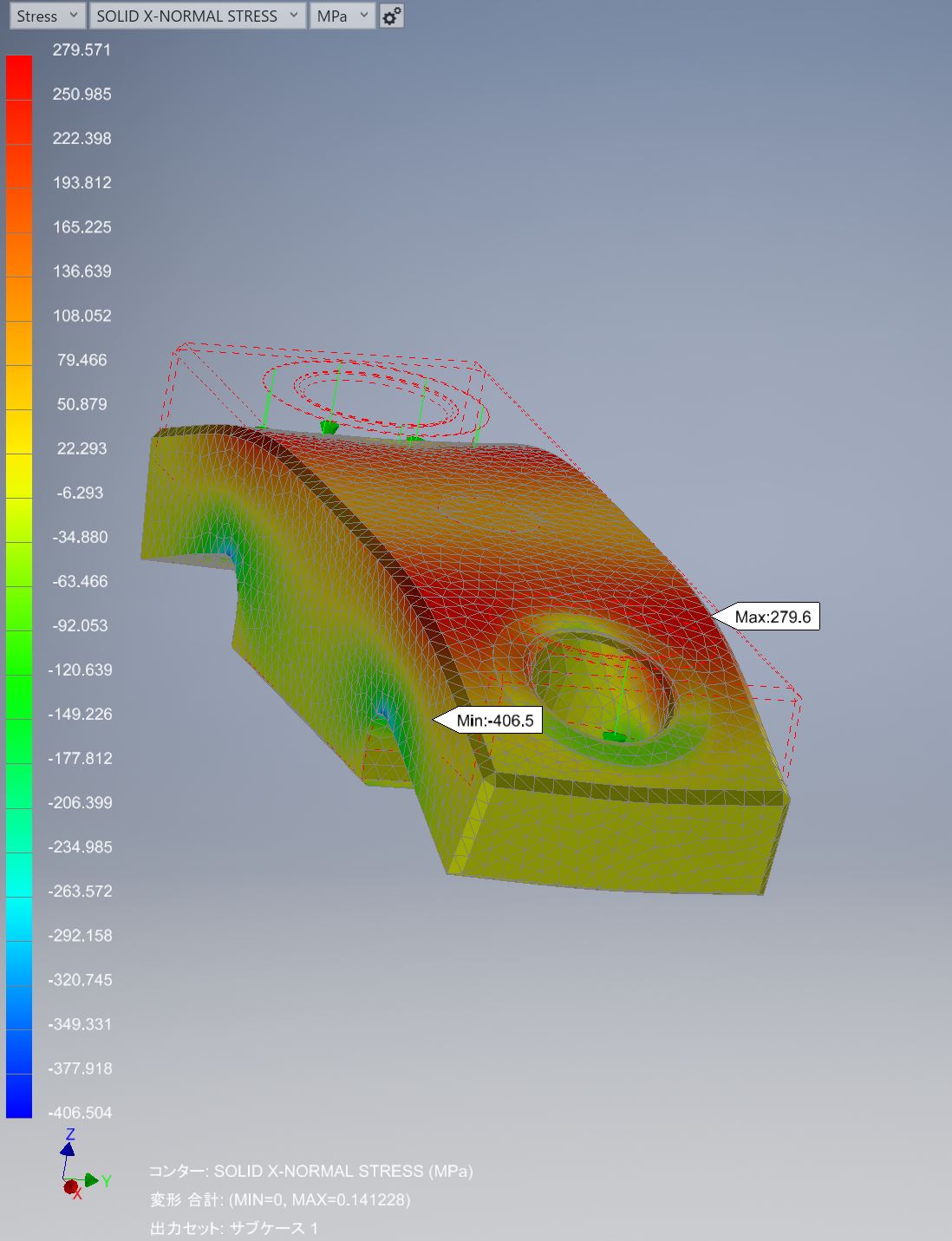↑Ｘ軸主応力で見ると片持ち梁の曲げみたいになってますね。
引張側で280[MPa]、圧縮側で407[MPa]。
S45C熱処理品ならギリギリいける感じかな？
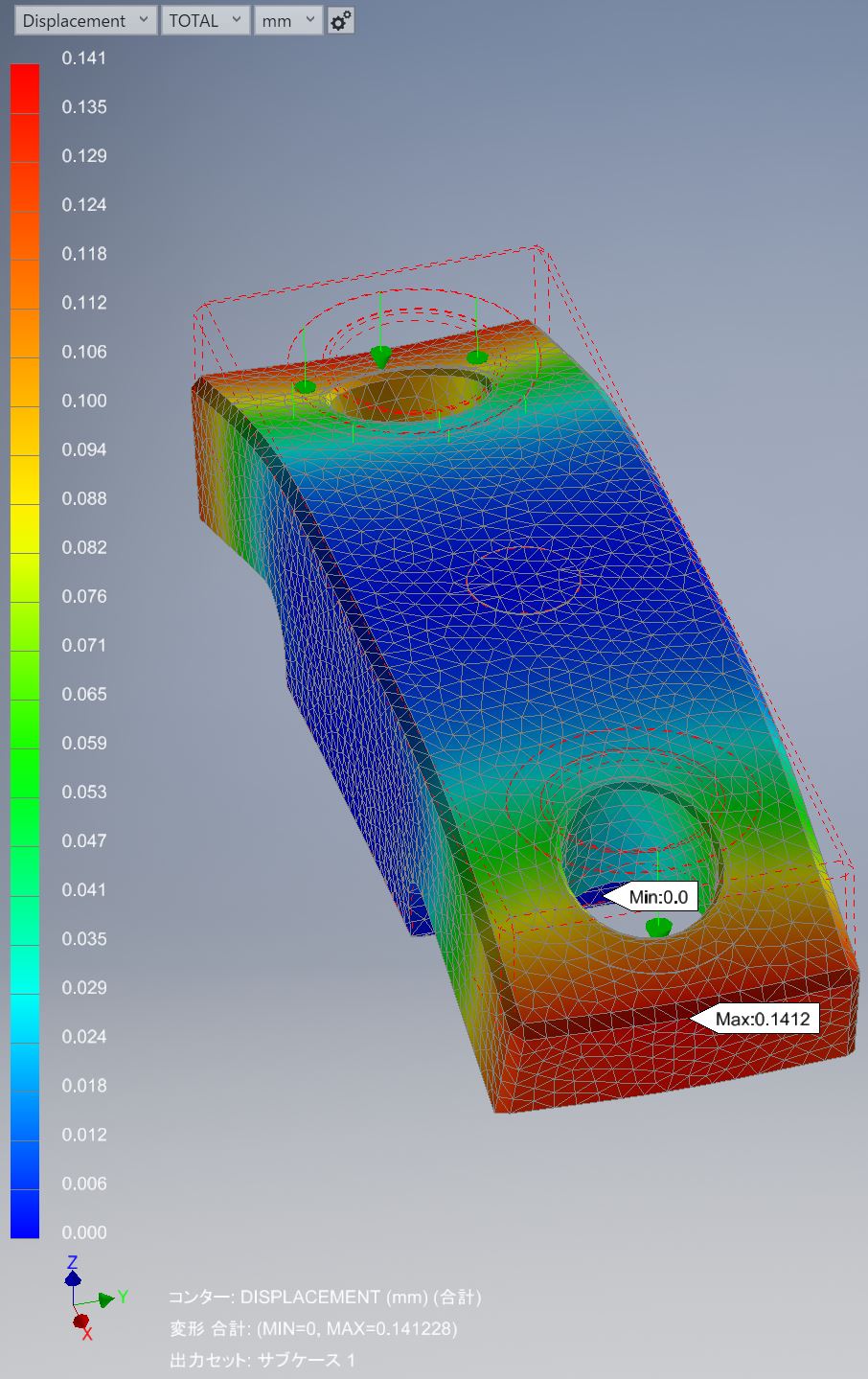↑最大変位は0.141[mm]です。
↑本命のＺ方向最大変位を確認します。0.138[mm]になっていますね。
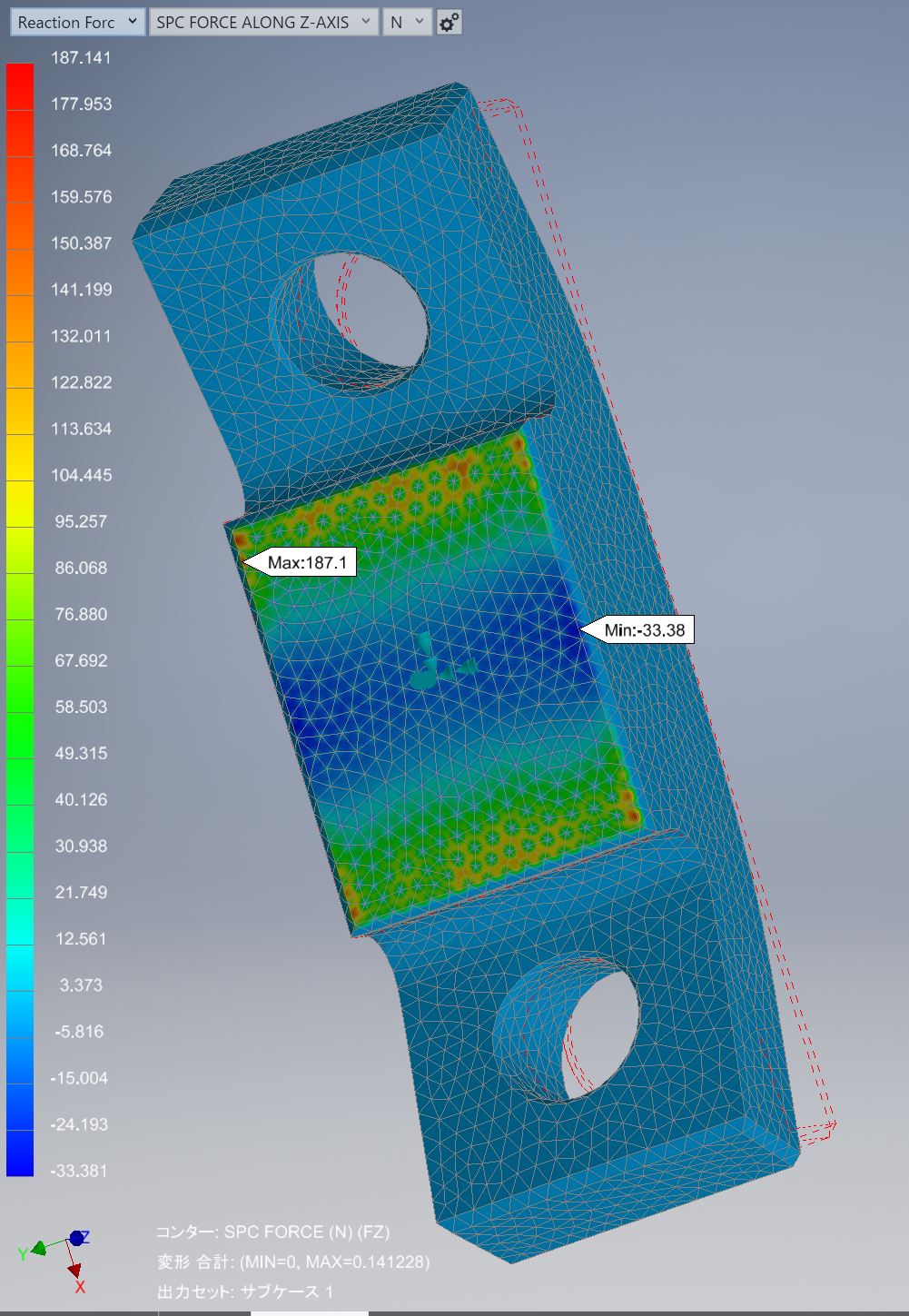↑ついでに固定拘束部の反力の傾向も見ておきましょう。
やはりエッジ部に集中している感じですね。
というわけで、被締結物(上側)の無外力時の見かけ上の圧縮ばね定数ですが、
ボルト軸力 17500[N] に対して Ｚ方向最大変位 0.138[mm] ですので、
Cc = 17500[N] / 0.138[mm] = 126.8[kN/mm]
となります。
22[mm]の板をベタで被締結物にした場合と比べるとだいたい１桁小さいですね。
被締結物(下)の圧縮ばね定数が相対的に大きい(たぶん3000[kN/mm]前後ぐらいになる)ので、被締結物の合計の圧縮ばね定数は126.8[kN/mm]としてしまってもいいでしょう。
※実設計時はきちんと計算しましょうね。
※※この結果を見ると、管フランジってけっこう微妙なことしてるんだな、ってなりますね。
＜５．見かけの圧縮ばね定数から内外力比と軸力変化を求める。＞
あとは普通の流れで内外力比を求めていきます。
[VDI2230によるボルトのばね定数 Cb]
1/Cb = 1/Eb * ( Lsk/An + La1/An + Ls/Ad3 + 0.5d/Ad3 )
+ 0.4d/(Em・An)
Cb = 241.56[kN/mm]
Cb : ばね定数[kN/mm]
Eb : ボルト材質のヤング率[GPa]
Lsk : ボルト頭部の等価長さ[mm]
※Lsk = 0.4d(六角穴付ボルトの場合)
La1 : ボルト非ねじ部の長さ[mm]
An : ボルト非ねじ部の断面積[mm^2]
Ls : ボルトねじ部の長さ[mm]
Ad3 : ボルトねじ部の有効断面積[mm^2]
d : ボルト非ねじ部の径[mm]
Em : ナット材質のヤング率[GPa]
[外力による軸力変化]
ΔF = ( Cb / (Cb + Cc) )・ Qa
ΔF = ( 241.56 / (241.56 + 126.8) * 5000
= 3278[N]
ΔF : 軸力の変化分[N]
Qa : 外力[N]
(Cb/(Cb+Cc)) : 内外力比
Cb : ボルトのばね定数[kN/mm]
Cc : 被締結物のばね定数[kN/mm]
えらいことになりましたね。
被締結物の見かけの圧縮ばね定数が１桁低いので、被締結物が負担していたであろう荷重の大部分がボルト軸力変化にもっていかれることになりました。
締結軸力 17500[N] + 軸力変化分 3278[N] = 外力作用時の軸力 20278[N] で、
M12の最大軸力は25000[N] なのでまだセーフですが、締付トルク誤差による締付け時軸力の誤差を考えるとほとんどマージンがなくなる感じになります。
あと、線形静解析をまわしている段階で気がついていたのですが、ここまで被締結物側のばね定数が低いと外力の作用位置による補正もなにもあったものではないですね。。。
＜６．板厚を変えて試してみる＞
板厚を変えてやってみました。22[mm]の材から10[mm]削った設計でしたが、これを38[mm]の材から削った形にしてみました。
Ｚ方向最大変位は 0.025[mm] ですので、
Cc = 17500[N] / 0.025[mm] = 700[kN/mm]
となり、ボルトのばね定数は241.56[kN/mm] なので、
5000[N]に対しての軸力変化は 1283[N]です。
他にもいくつかやってみました。
結果は下記です。
※こうやって少しずつ寸法変えて試せるのはInventorとくっついてるAutodesk Nastranのいいところですね。
材の板厚[mm] ：22 30 38 50
フランジ部の板厚[mm] ：12 20 28 40
Ｚ方向最大変位[mm] ：0.138 0.048 0.025 0.016
ばね定数[kN/mm] ：126.8 364.6 700 1094
軸力変化[N] ：3278 1993 1283 904.3
材の板厚を50[mm]までひっぱってもばね定数は1094[kN/mm]どまりです。
＜７．やってはいけない設計ではないが……＞
さて、ここまで「やってはいけない設計？」な図を元に具体的な数字を置いて検討してき
たわけですが、板厚を積んでいっても被締結物のばね定数はとうてい3000[kN/mm]に届きません。そのため内外力比が大きくなり、軸力の変化分は外力に対して大きくなります。
これは逆に言えば締結体の面圧を低下させるのに使われる荷重が小さくなることになります。
今回の例でいけば、接触部の面積は40[mm]x32[mm]=1280[mm2]ですので、
材の板厚22[mm]では締結体の面圧を低下させるのに使われる外力は1722[N]で、面圧の低下は1.34[MPa]です。
材の板厚50[mm]の場合は締結体の面圧を低下させるのに使われる外力は4096[N]なので、面圧の低下は3.20[MPa]です。
JIS等のガスケットを挟んだ管フランジ締結体でこの構造が採用されているのはおそらくここが理由ではないかと思います。管フランジ締結体では内部流体がガスケット面から漏洩するのを避けることが優先されますので、管フランジがついた配管が線膨張等で変形し、管フランジに対して大きな荷重がかかった場合でもガスケット面圧を下げる量が比較的少なく、かわりにボルトの軸力が増加するというバランスが選択されたのではないかと考えられます。
JIS等の管フランジ締結体は規格制定時の計算と長年の経験から、所定の使用条件下であれば問題なく使える設計となっています。
さて、新規設計の場合はどうかというと、わざわざFEMをかけて見かけの圧縮ばね定数を確認して計算するほどの用途であれば、採用してもいいのではないでしょうか。特に面圧の低下が致命傷となるような領域ではボルトの軸力変化を適切に設定できれば有効な構造だといえるでしょう。
一方、相対的な面圧低下の影響がそれほどシビアではない用途、つまり一般的なボルト締結体の用途であれば、「やってはいけない」ことはないですが、「わざわざ選択するほどでもない」構造ではないかと思います。
そして、FEMをわざわざかけて確認する必要を考えると、設計コスト面からは「避けた方がいいんじゃないかな？」という構造とも言えるのではないでしょうか。
これを見て自分がしたTweetが下記です。
---------
（「やってはいけない設計」みたいなのが流れてきたが、
管フランジ締結体を全否定されてる感じだし、
実際の寸法形状と使用環境・運用による、だと思いますね。
数字置いてみるまではわかんなやつ。
ただ計算めんどいので避けれるなら避けたほうがいい、
という話ならわかります。）
---------
で、Tweetした後に、これ単純に
「外力の作用位置と被締結物のばね定数」
の話だよなあ、となりまして。
つまり、ちょうどいい題材がやってきた感じですね。
＜２．おさらい＞
話をすすめる前にざっくりとボルト締結体の考え方のおさらいです。
・M5～M16ぐらいの機械構造用六角ボルトには標準的な締付け軸力がある。
・ボルト締結体に外力が作用した場合、
この外力はボルト軸力増加分と被締結物の圧縮(曲げ)変形分に按分される。
・外力の按分具合は内外力比という比率で決まる。
・被締結物の圧縮ばね定数とボルトの引張ばね定数で内外力比が決まる。
・内外力比は外力作用位置／軸力作用位置によって修正され、
ボルト軸から外力作用位置まで距離がある場合、
修正係数は0.15前後の低い値になることがある。
・修正係数は適用範囲が限られたいくつかの実験式があるだけで、
理論的あるいは定量的に求めることは難しい。
詳細は下の過去記事を参照してください。長くて読みにくいですけど。
「ボルト締結体の検討（その１）」
http://kirikuzudo.sblo.jp/article/187148956.html
「ボルト締結体の検討（その２）」
http://kirikuzudo.sblo.jp/article/187194450.html
「六角ポルトの強度区分について」
http://kirikuzudo.sblo.jp/article/187638425.html
＜３．数値解析で被締結物(上)の圧縮ばね定数を求める＞
今回は下の考え方を試してみます。
・修正係数を用いずに被締結物の見かけの圧縮ばね定数を、
数値解析(Nastran等のFEM)を用いて求めることで
実用的な内外力比を得られる(要検証)
TLに流れてきた図のような複雑な形状について、
修正係数を理論的に求めるのは難しいと思います。
そして、そもそもなぜ修正係数が必要かというかと、ざっくりした言い方をすれば、
「外力作用位置や軸力作用位置によって
被締結物の見かけの圧縮ばね定数が変化するから」
です。
逆に考えれば、変化した被締結物の見かけの圧縮ばね定数がわかるのであれば修正係数を使わないで済ますことができます。
そこで、数値解析でボルト軸力および外力を荷重としてかけたときのＺ方向最大変位をもとに、被締結物の見かけの圧縮ばね定数を求め、これを使って内力係数を決定することにします。
TLに流れてきた図は具体的な寸法が入っていなかったので、下図のように寸法を決めておきます。ボルトはM12 x 60Lです。
これを元にAutodesk InventorでNastran用のモデルを作ります。
※フィレット半径はFEMかけながらフォンミーゼス応力を見て6[mm]にしました。
Nastranで次の条件を入れて線形静解析をかけます。
・メッシュ設定はParabolic 2[mm]
・荷重はボルトの座の部分で受けます
・T字の底面を固定拘束
・荷重はM12のT系列標準軸力17500[N]
・外力はＺ(+)方向に5000[N]
＜４．Autodesk Nastranでの線形静解析の結果＞
結果は以下になります。
↑フォンミーゼス応力でフィレット部が424[MPa]にいってますね。
↑Ｘ軸主応力で見ると片持ち梁の曲げみたいになってますね。
引張側で280[MPa]、圧縮側で407[MPa]。
S45C熱処理品ならギリギリいける感じかな？
↑最大変位は0.141[mm]です。
↑本命のＺ方向最大変位を確認します。0.138[mm]になっていますね。
↑ついでに固定拘束部の反力の傾向も見ておきましょう。
やはりエッジ部に集中している感じですね。
というわけで、被締結物(上側)の無外力時の見かけ上の圧縮ばね定数ですが、
ボルト軸力 17500[N] に対して Ｚ方向最大変位 0.138[mm] ですので、
Cc = 17500[N] / 0.138[mm] = 126.8[kN/mm]
となります。
22[mm]の板をベタで被締結物にした場合と比べるとだいたい１桁小さいですね。
被締結物(下)の圧縮ばね定数が相対的に大きい(たぶん3000[kN/mm]前後ぐらいになる)ので、被締結物の合計の圧縮ばね定数は126.8[kN/mm]としてしまってもいいでしょう。
※実設計時はきちんと計算しましょうね。
※※この結果を見ると、管フランジってけっこう微妙なことしてるんだな、ってなりますね。
＜５．見かけの圧縮ばね定数から内外力比と軸力変化を求める。＞
あとは普通の流れで内外力比を求めていきます。
[VDI2230によるボルトのばね定数 Cb]
1/Cb = 1/Eb * ( Lsk/An + La1/An + Ls/Ad3 + 0.5d/Ad3 )
+ 0.4d/(Em・An)
Cb = 241.56[kN/mm]
Cb : ばね定数[kN/mm]
Eb : ボルト材質のヤング率[GPa]
Lsk : ボルト頭部の等価長さ[mm]
※Lsk = 0.4d(六角穴付ボルトの場合)
La1 : ボルト非ねじ部の長さ[mm]
An : ボルト非ねじ部の断面積[mm^2]
Ls : ボルトねじ部の長さ[mm]
Ad3 : ボルトねじ部の有効断面積[mm^2]
d : ボルト非ねじ部の径[mm]
Em : ナット材質のヤング率[GPa]
[外力による軸力変化]
ΔF = ( Cb / (Cb + Cc) )・ Qa
ΔF = ( 241.56 / (241.56 + 126.8) * 5000
= 3278[N]
ΔF : 軸力の変化分[N]
Qa : 外力[N]
(Cb/(Cb+Cc)) : 内外力比
Cb : ボルトのばね定数[kN/mm]
Cc : 被締結物のばね定数[kN/mm]
えらいことになりましたね。
被締結物の見かけの圧縮ばね定数が１桁低いので、被締結物が負担していたであろう荷重の大部分がボルト軸力変化にもっていかれることになりました。
締結軸力 17500[N] + 軸力変化分 3278[N] = 外力作用時の軸力 20278[N] で、
M12の最大軸力は25000[N] なのでまだセーフですが、締付トルク誤差による締付け時軸力の誤差を考えるとほとんどマージンがなくなる感じになります。
あと、線形静解析をまわしている段階で気がついていたのですが、ここまで被締結物側のばね定数が低いと外力の作用位置による補正もなにもあったものではないですね。。。
＜６．板厚を変えて試してみる＞
板厚を変えてやってみました。22[mm]の材から10[mm]削った設計でしたが、これを38[mm]の材から削った形にしてみました。
Ｚ方向最大変位は 0.025[mm] ですので、
Cc = 17500[N] / 0.025[mm] = 700[kN/mm]
となり、ボルトのばね定数は241.56[kN/mm] なので、
5000[N]に対しての軸力変化は 1283[N]です。
他にもいくつかやってみました。
結果は下記です。
※こうやって少しずつ寸法変えて試せるのはInventorとくっついてるAutodesk Nastranのいいところですね。
材の板厚[mm] ：22 30 38 50
フランジ部の板厚[mm] ：12 20 28 40
Ｚ方向最大変位[mm] ：0.138 0.048 0.025 0.016
ばね定数[kN/mm] ：126.8 364.6 700 1094
軸力変化[N] ：3278 1993 1283 904.3
材の板厚を50[mm]までひっぱってもばね定数は1094[kN/mm]どまりです。
＜７．やってはいけない設計ではないが……＞
さて、ここまで「やってはいけない設計？」な図を元に具体的な数字を置いて検討してき
たわけですが、板厚を積んでいっても被締結物のばね定数はとうてい3000[kN/mm]に届きません。そのため内外力比が大きくなり、軸力の変化分は外力に対して大きくなります。
これは逆に言えば締結体の面圧を低下させるのに使われる荷重が小さくなることになります。
今回の例でいけば、接触部の面積は40[mm]x32[mm]=1280[mm2]ですので、
材の板厚22[mm]では締結体の面圧を低下させるのに使われる外力は1722[N]で、面圧の低下は1.34[MPa]です。
材の板厚50[mm]の場合は締結体の面圧を低下させるのに使われる外力は4096[N]なので、面圧の低下は3.20[MPa]です。
JIS等のガスケットを挟んだ管フランジ締結体でこの構造が採用されているのはおそらくここが理由ではないかと思います。管フランジ締結体では内部流体がガスケット面から漏洩するのを避けることが優先されますので、管フランジがついた配管が線膨張等で変形し、管フランジに対して大きな荷重がかかった場合でもガスケット面圧を下げる量が比較的少なく、かわりにボルトの軸力が増加するというバランスが選択されたのではないかと考えられます。
JIS等の管フランジ締結体は規格制定時の計算と長年の経験から、所定の使用条件下であれば問題なく使える設計となっています。
さて、新規設計の場合はどうかというと、わざわざFEMをかけて見かけの圧縮ばね定数を確認して計算するほどの用途であれば、採用してもいいのではないでしょうか。特に面圧の低下が致命傷となるような領域ではボルトの軸力変化を適切に設定できれば有効な構造だといえるでしょう。
一方、相対的な面圧低下の影響がそれほどシビアではない用途、つまり一般的なボルト締結体の用途であれば、「やってはいけない」ことはないですが、「わざわざ選択するほどでもない」構造ではないかと思います。
そして、FEMをわざわざかけて確認する必要を考えると、設計コスト面からは「避けた方がいいんじゃないかな？」という構造とも言えるのではないでしょうか。
