切屑堂 kirikuzudo
ブログ： 2020/02/11 ボルト締結体の検討（その１）
ばね座金ってあんまし意味ないよね、の話から転じて、少しボルト締結体の検討をしてみたいと思います。といっても、検討の流れを追うだけです。式の導出とか解説とかは参考資料を読んでもらうとして、というやつです。また、細かい数字は丸めたり大胆に省略したりしてるので、真面目な検討するときは参考資料とかVDI2230とかを使ってきっかりやってください。
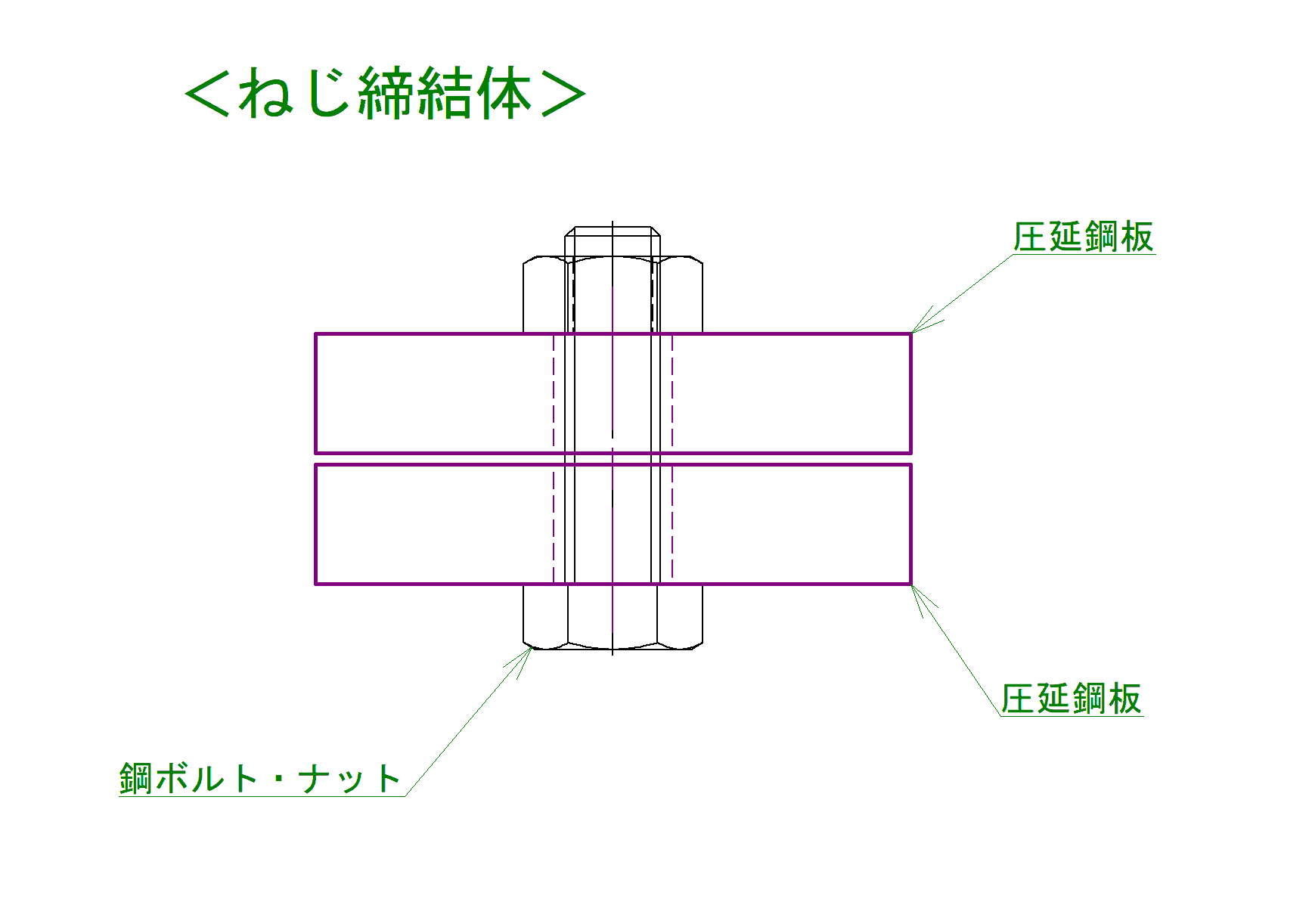
ここでは下の図のようなボルトとナットによる締結体を前提にしています。ボルトとナットはメートル並目ねじ M8 とし、t6.0の圧延鋼板２枚の締結で検討していきたいと思います。ボルトはSCM435製の強度区分10.9の六角穴付ボルトとし、ナットはS45C(H)の強度区分8T品(8.8相当)とします
＜１．軸力と締付けトルクの関係＞
トルクレンチでボルトの締付けを管理する話はよく聞くと思います。ですが、締付けトルクとボルトにかかる軸力はそのまま対応しているわけではありません。締付けトルクとボルトにかかる軸力の関係は下記の式で表現されます。
Ts = F・(μs・d・secα' + P/6.28 )
Ts : 締付けトルク[N・m]
F : 軸力[N]
μs : ねじ面の摩擦係数
d : ボルトの有効径[m]
α' : フランク角
※並目メートルねじではフランク角が30[deg]
※sec(30[deg]) = 1.1547
P : ねじピッチ[m]
この式から同じ軸力でも、
・ピッチが大きい
・有効径が大きい
・摩擦係数が大きい
ほうが締付けトルクは大きくなります。括弧内をまとめて「トルク係数」と呼ぶこともあります。
さて、今回の検討例にあてはめてみましょう。
メートル並目ねじM8で、標準軸力はボルト・ナットが8Tのため1.8T系列となるので、F=14060[N]となります。
※標準軸力は下記の技術資料を参照しました。
東日製作所 ダウンロード 技術資料
https://www.tohnichi.co.jp/download_services
ねじ面の摩擦係数はモリブデングリスを使って0.1とします。
※実際にはモリブデングリスでは摩擦家数は0.09～0.12とばらつきます
ボルトの有効径は7.19[mm]とし、ねじピッチはM8並目なので1.25[mm]です。
以上より、締付けトルクTs=14.5[N・m]となります。
（無潤滑だと摩擦係数が0.2程度になり、締付けトルクは26.1[N・m]程度になります）
＜宣伝＞
トルク係数を安定化するすごい製品だ！
東日製作所 軸力安定化剤 Fcon
https://www.tohnichi.co.jp/products/detail/81
＜／宣伝＞
＜２．ねじ部の応力＞
ねじ部にかかる応力は
・ボルトが長手方向に引っ張られる引張応力
・ねじ面および座面の摩擦に起因する、ボルトのねじりから発生するせん断応力
の２つにわけられます。
（今回はボルトに曲げモーメントがかかっていないと仮定して話をします。）
引張応力は下記の式で表されます。
σf = F / As
σf : 引張応力[MPa]
F : 軸力[N]
As : ボルトの引張有効断面積[mm^2]
※今回はAsは谷底径の断面積の90％で近似します
また、ねじりによるせん断応力は欠きの式で表されます。
τt = 16・Ts / (6.28 x ds^3)
τt : せん断応力[MPa]
Ts : 締付けトルク[N・mm]
ds : ボルトの谷底径[mm]
※単位に注意です。
※締付けトルクは[1]の式で軸力に換算できます。
さて、今回の検討例にあてはめてみましょう。
M8並目のボルト谷径を6.6[mm]、前項から締付けトルクTs=14.5[N・m]、軸力F=14060[N]となっていますので、上の式を使って、引張応力σf=411[MPa]、せん断応力τt=129[MPa]となります。
＜３．ねじ部の応力基準＞
ミーゼス応力が材料の降伏応力に達したときに降伏すると仮定します。材料の降伏基準は条件によって異なりますが、通常のボルトはこれで攻めても問題ないと思います。ボルトのミーゼス応力は引張応力とせん断応力から次の式で求めることができます。
σeq = (σf ^2 + 3 x τt ^2 ) ^ 0.5
σeq : ミーゼス応力[MPa]
σf : 引張応力[MPa]
τt : せん断応力[MPa]
せん断応力はねじ谷底の径で最大になるため、上の式のσeq はねじ谷底表面が降伏しはじめるミーゼス応力を表しています。（全断面降伏を基準にするともうちょっと緩くなりますが計算がめっちゃめんどいらしいのでやめました）
一般的なSCM435製の六角穴付ボルトは強度区部が10.9で、材料の降伏応力σy = 900[MPa]となります。
一般のトルク法によるボルト締付けでは降伏点の60[％]程度の応力で締め付けることが多く、下記を満たせばボルトを安全な領域で使用できることになります。
σeq ＜ σy * 0.6
これにより、強度区分10.9の六角穴付ボルトであればσeq ＜ 540[MPa] であれば安全と言えます。
さて、今回の検討例にあてはめてみましょう。
前項で引張応力σf=411[MPa]、せん断応力τt=129[MPa]となっていますので、ここからミーゼス応力σeq = 467[MPa] となります。これは540[MPa]を下回っていますので安全と言えますが、静的な締付けだけの状態ですし、標準軸力はこの状態を元にしていますので、ここまでは検算みたいなものだといえます。
＜４．ばね定数＞
さて、ここまではボルトとナットで金具を締付けた状態の話をしてきました。ここからこの金具を引きはがす方向に垂直に引張荷重（外力）がかかった話になります。外から金具にかかる荷重なので「外力」といいます。これに対して、ボルトを締結している力を「内力」といいます。
外からかかった引張荷重のどれだけが軸力を増やすことにつながるかを計算するためにはボルトと締結体の変位をからめた不静定問題を解かなければいけません。
※不静定問題、めんどいやつです。材料力学の最初の山ですね。
高専の機械工学科ではこれを落として留年した人は数知れません。
が、先人がそういう面倒がないような方法を確立してくれています。それが「ばね定数」を使って「内外力比」を求める方法です。
以下の式でボルトと被締結物の「ばね定数」を求めます。
[VDI2230によるボルトのばね定数 Cb]
1/Cb = 1/Eb * ( Lsk/An + La1/An + Ls/Ad3 + 0.5d/Ad3 )
+ 0.4d/(Em・An)
Cb : ばね定数[kN/mm]
Eb : ボルト材質のヤング率[GPa]
Lsk : ボルト頭部の等価長さ[mm]
※Lsk = 0.4d(六角穴付ボルトの場合)
La1 : ボルト非ねじ部の長さ[mm]
An : ボルト非ねじ部の断面積[mm^2]
Ls : ボルトねじ部の長さ[mm]
Ad3 : ボルトねじ部の有効断面積[mm^2]
d : ボルト非ねじ部の径[mm]
Em : ナット材質のヤング率[GPa]
※参考資料には「ボルト細径部」の項がありますが、ここでは非ねじ部のある一般的な六角穴付ボルトを対象とするために細径部の長さ=0[mm]として項自体を省いています。
[VDI2230による被締結物のばね定数 Cc]
Dc = (Ec/Lg)・(π/4)
・[( Do^2 - Dh^2 ) + Do・Lg・{ (x + 1)^2 - 1 }]
x = [ Lg・Do / ( Lg + Do )^2 ]^0.333
Cc : ばね定数[kN/mm]
Ec : 被締結物のヤング率[GPa]
Lg : 被締結物の厚さ[mm]
Do : ボルト座面径[mm]
Dh : ボルト穴径[mm]
さて、今回の検討例にあてはめてみましょう。
ボルトとナットはメートル並目ねじ M8 とし、t6.0の圧延鋼板２枚の締結です。
ボルト寸法はM8 x 25Lとして、非ねじ部のない全ねじを使用します。
まずボルトのばね定数Cbです。
ボルトの非ねじ部径としてd=6.6[mm]を使用します。ヤング率はEb,Em=200[GPa]。非ねじ部は0[mm]でねじ部は25[mm]、ねじ部の有効断面積は径を6.6[mm]として計算します。
1/Cb = 0.005 * ( 0.0772 + 0.7311 + 0.0965 ) + 0.005 * ( 0.0772 )
Cb = 203.67[kN/mm]
次に被締結物のばね定数です。
x = [ 12 x 13 / ( 12 + 13 )^2 ]^0.333 = 0.63
Cc = (200/12) x (3.14/4) x [(169 - 73.96) + 13 x 12 x 1.6569]
= 4625.17[kN/mm]
以上より、
・ボルトのばね定数 Cb = 203.67[kN/mm]
・被締結物のばね定数 Cc = 4625.17[kN/mm]
となります。
＜５．外力の作用＞
ばね定数を用いて内外力比から外力が作用した場合の軸力変化を計算できます。ばね定数を使用して外力から軸力変化を求める式は下記になります。
ΔF = ( Cb / (Cb + Cc) )・ Qa
ΔF : 軸力の変化分[N]
Qa : 外力[N]
(Cb/(Cb+Cc)) : 内外力比
Cb : ボルトのばね定数[kN/mm]
Cc : 被締結物のばね定数[kN/mm]
さて、今回の検討例にあてはめてみましょう。
作用する外力は単純にボルト軸の方向への引張で1[kN]とします。
前項から
・ボルトのばね定数 Cb = 203.67[kN/mm]
・被締結物のばね定数 Cc = 4625.17[kN/mm]
なので、
ΔF = (203.67 / (203.67 + 4625.17) ) * 10000 = 42.18[N]
となり、外力の4.2[％]程度しか軸力は変化しないことがわかります。
このように大きな外力がかかっても被締結物のばね定数が大きければボルトの軸力変化はわずかになります。
＜６．ねじ部の応力の再検討＞
第２項でねじ部にかかる応力を検討しました。ここで前項の外力による軸力変化を第２項の応力検討に反映します。
外力は単純な引張によるものなので、必要なのは引張応力の再検討だけです。
σf = F / As
σf : 引張応力[MPa]
F : 軸力[N]
As : ボルトの引張有効断面積[mm^2]
※今回はAsは谷底径の断面積の90％で近似します
M8並目のボルト谷径を6.6[mm]、締付けによる標準軸力F=14060[N]、さらに軸力変化ΔF=42[N]となっていますので、上の式を使って、引張応力σf=412[MPa]と更新されます。
1[MPa]しか変わっていないのでこれは完全にセーフですね。
＜７．どこまで大きな外力に耐えられるのか＞
被締結物を2枚の圧延鋼板t6.0としましたが、これが外力により変形しないと仮定しましょう。（t6.0に10[kN]を入れたらたぶんけっこうな弾性変形を起こします。）
第３項のの検討でミーゼス応力σeq=540[MPa]までは安全という話になっていました。せん断応力τt=129[MPa]は変わらないとして、ミーゼス応力σeq=540[MPa]と置くと、その場合の引張応力は、
σf = ( σeq^2 - 3 x τt^2 )^0.5 = 492[MPa]
となります。締付けによる軸力での応力は411[MPa]でしたので、差分は81[MPa]あります。有効径の断面積をこれに積算することで、ボルトの軸力変化の許容値がわかります。
Δf(safe) = 81[MPa] x 34.2[mm^2] = 2770[N]
Qa = ΔF(safe) / ( Cb / (Cb + Cc) )
= 2770[N] / (203.67 / (203.67 + 4625.17) ) = 65674[N](6.7[tonf])
被締結物の強度を無視すると、ボルト自体は6.7トンもの外力がかかっても耐えられる計算になります。
まあ、これは単純に引張しか作用しない実験室的な状況で、被締結物の強度を無視した結果ですので、結果として緩すぎるわけですが、M8並目のボルト・ナットは被締結物との関係次第ではずいぶんと大きな荷重を伝達できることがわかります。
---------
とりあえず（その１）はこのあたりまでにします。
（その２）以降では強度区分が低い場合や被締結物の板厚、あと疲労の話などをできればなあ、とか思います。
（エターしないようがんばります。）
※参考文献
『トラブルを未然に防ぐ ねじ設計法と保全対策』
https://www.amazon.co.jp/dp/4526072583/
＜１．軸力と締付けトルクの関係＞
トルクレンチでボルトの締付けを管理する話はよく聞くと思います。ですが、締付けトルクとボルトにかかる軸力はそのまま対応しているわけではありません。締付けトルクとボルトにかかる軸力の関係は下記の式で表現されます。
Ts = F・(μs・d・secα' + P/6.28 )
Ts : 締付けトルク[N・m]
F : 軸力[N]
μs : ねじ面の摩擦係数
d : ボルトの有効径[m]
α' : フランク角
※並目メートルねじではフランク角が30[deg]
※sec(30[deg]) = 1.1547
P : ねじピッチ[m]
この式から同じ軸力でも、
・ピッチが大きい
・有効径が大きい
・摩擦係数が大きい
ほうが締付けトルクは大きくなります。括弧内をまとめて「トルク係数」と呼ぶこともあります。
さて、今回の検討例にあてはめてみましょう。
メートル並目ねじM8で、標準軸力はボルト・ナットが8Tのため1.8T系列となるので、F=14060[N]となります。
※標準軸力は下記の技術資料を参照しました。
東日製作所 ダウンロード 技術資料
https://www.tohnichi.co.jp/download_services
ねじ面の摩擦係数はモリブデングリスを使って0.1とします。
※実際にはモリブデングリスでは摩擦家数は0.09～0.12とばらつきます
ボルトの有効径は7.19[mm]とし、ねじピッチはM8並目なので1.25[mm]です。
以上より、締付けトルクTs=14.5[N・m]となります。
（無潤滑だと摩擦係数が0.2程度になり、締付けトルクは26.1[N・m]程度になります）
＜宣伝＞
トルク係数を安定化するすごい製品だ！
東日製作所 軸力安定化剤 Fcon
https://www.tohnichi.co.jp/products/detail/81
＜／宣伝＞
＜２．ねじ部の応力＞
ねじ部にかかる応力は
・ボルトが長手方向に引っ張られる引張応力
・ねじ面および座面の摩擦に起因する、ボルトのねじりから発生するせん断応力
の２つにわけられます。
（今回はボルトに曲げモーメントがかかっていないと仮定して話をします。）
引張応力は下記の式で表されます。
σf = F / As
σf : 引張応力[MPa]
F : 軸力[N]
As : ボルトの引張有効断面積[mm^2]
※今回はAsは谷底径の断面積の90％で近似します
また、ねじりによるせん断応力は欠きの式で表されます。
τt = 16・Ts / (6.28 x ds^3)
τt : せん断応力[MPa]
Ts : 締付けトルク[N・mm]
ds : ボルトの谷底径[mm]
※単位に注意です。
※締付けトルクは[1]の式で軸力に換算できます。
さて、今回の検討例にあてはめてみましょう。
M8並目のボルト谷径を6.6[mm]、前項から締付けトルクTs=14.5[N・m]、軸力F=14060[N]となっていますので、上の式を使って、引張応力σf=411[MPa]、せん断応力τt=129[MPa]となります。
＜３．ねじ部の応力基準＞
ミーゼス応力が材料の降伏応力に達したときに降伏すると仮定します。材料の降伏基準は条件によって異なりますが、通常のボルトはこれで攻めても問題ないと思います。ボルトのミーゼス応力は引張応力とせん断応力から次の式で求めることができます。
σeq = (σf ^2 + 3 x τt ^2 ) ^ 0.5
σeq : ミーゼス応力[MPa]
σf : 引張応力[MPa]
τt : せん断応力[MPa]
せん断応力はねじ谷底の径で最大になるため、上の式のσeq はねじ谷底表面が降伏しはじめるミーゼス応力を表しています。（全断面降伏を基準にするともうちょっと緩くなりますが計算がめっちゃめんどいらしいのでやめました）
一般的なSCM435製の六角穴付ボルトは強度区部が10.9で、材料の降伏応力σy = 900[MPa]となります。
一般のトルク法によるボルト締付けでは降伏点の60[％]程度の応力で締め付けることが多く、下記を満たせばボルトを安全な領域で使用できることになります。
σeq ＜ σy * 0.6
これにより、強度区分10.9の六角穴付ボルトであればσeq ＜ 540[MPa] であれば安全と言えます。
さて、今回の検討例にあてはめてみましょう。
前項で引張応力σf=411[MPa]、せん断応力τt=129[MPa]となっていますので、ここからミーゼス応力σeq = 467[MPa] となります。これは540[MPa]を下回っていますので安全と言えますが、静的な締付けだけの状態ですし、標準軸力はこの状態を元にしていますので、ここまでは検算みたいなものだといえます。
＜４．ばね定数＞
さて、ここまではボルトとナットで金具を締付けた状態の話をしてきました。ここからこの金具を引きはがす方向に垂直に引張荷重（外力）がかかった話になります。外から金具にかかる荷重なので「外力」といいます。これに対して、ボルトを締結している力を「内力」といいます。
外からかかった引張荷重のどれだけが軸力を増やすことにつながるかを計算するためにはボルトと締結体の変位をからめた不静定問題を解かなければいけません。
※不静定問題、めんどいやつです。材料力学の最初の山ですね。
高専の機械工学科ではこれを落として留年した人は数知れません。
が、先人がそういう面倒がないような方法を確立してくれています。それが「ばね定数」を使って「内外力比」を求める方法です。
以下の式でボルトと被締結物の「ばね定数」を求めます。
[VDI2230によるボルトのばね定数 Cb]
1/Cb = 1/Eb * ( Lsk/An + La1/An + Ls/Ad3 + 0.5d/Ad3 )
+ 0.4d/(Em・An)
Cb : ばね定数[kN/mm]
Eb : ボルト材質のヤング率[GPa]
Lsk : ボルト頭部の等価長さ[mm]
※Lsk = 0.4d(六角穴付ボルトの場合)
La1 : ボルト非ねじ部の長さ[mm]
An : ボルト非ねじ部の断面積[mm^2]
Ls : ボルトねじ部の長さ[mm]
Ad3 : ボルトねじ部の有効断面積[mm^2]
d : ボルト非ねじ部の径[mm]
Em : ナット材質のヤング率[GPa]
※参考資料には「ボルト細径部」の項がありますが、ここでは非ねじ部のある一般的な六角穴付ボルトを対象とするために細径部の長さ=0[mm]として項自体を省いています。
[VDI2230による被締結物のばね定数 Cc]
Dc = (Ec/Lg)・(π/4)
・[( Do^2 - Dh^2 ) + Do・Lg・{ (x + 1)^2 - 1 }]
x = [ Lg・Do / ( Lg + Do )^2 ]^0.333
Cc : ばね定数[kN/mm]
Ec : 被締結物のヤング率[GPa]
Lg : 被締結物の厚さ[mm]
Do : ボルト座面径[mm]
Dh : ボルト穴径[mm]
さて、今回の検討例にあてはめてみましょう。
ボルトとナットはメートル並目ねじ M8 とし、t6.0の圧延鋼板２枚の締結です。
ボルト寸法はM8 x 25Lとして、非ねじ部のない全ねじを使用します。
まずボルトのばね定数Cbです。
ボルトの非ねじ部径としてd=6.6[mm]を使用します。ヤング率はEb,Em=200[GPa]。非ねじ部は0[mm]でねじ部は25[mm]、ねじ部の有効断面積は径を6.6[mm]として計算します。
1/Cb = 0.005 * ( 0.0772 + 0.7311 + 0.0965 ) + 0.005 * ( 0.0772 )
Cb = 203.67[kN/mm]
次に被締結物のばね定数です。
x = [ 12 x 13 / ( 12 + 13 )^2 ]^0.333 = 0.63
Cc = (200/12) x (3.14/4) x [(169 - 73.96) + 13 x 12 x 1.6569]
= 4625.17[kN/mm]
以上より、
・ボルトのばね定数 Cb = 203.67[kN/mm]
・被締結物のばね定数 Cc = 4625.17[kN/mm]
となります。
＜５．外力の作用＞
ばね定数を用いて内外力比から外力が作用した場合の軸力変化を計算できます。ばね定数を使用して外力から軸力変化を求める式は下記になります。
ΔF = ( Cb / (Cb + Cc) )・ Qa
ΔF : 軸力の変化分[N]
Qa : 外力[N]
(Cb/(Cb+Cc)) : 内外力比
Cb : ボルトのばね定数[kN/mm]
Cc : 被締結物のばね定数[kN/mm]
さて、今回の検討例にあてはめてみましょう。
作用する外力は単純にボルト軸の方向への引張で1[kN]とします。
前項から
・ボルトのばね定数 Cb = 203.67[kN/mm]
・被締結物のばね定数 Cc = 4625.17[kN/mm]
なので、
ΔF = (203.67 / (203.67 + 4625.17) ) * 10000 = 42.18[N]
となり、外力の4.2[％]程度しか軸力は変化しないことがわかります。
このように大きな外力がかかっても被締結物のばね定数が大きければボルトの軸力変化はわずかになります。
＜６．ねじ部の応力の再検討＞
第２項でねじ部にかかる応力を検討しました。ここで前項の外力による軸力変化を第２項の応力検討に反映します。
外力は単純な引張によるものなので、必要なのは引張応力の再検討だけです。
σf = F / As
σf : 引張応力[MPa]
F : 軸力[N]
As : ボルトの引張有効断面積[mm^2]
※今回はAsは谷底径の断面積の90％で近似します
M8並目のボルト谷径を6.6[mm]、締付けによる標準軸力F=14060[N]、さらに軸力変化ΔF=42[N]となっていますので、上の式を使って、引張応力σf=412[MPa]と更新されます。
1[MPa]しか変わっていないのでこれは完全にセーフですね。
＜７．どこまで大きな外力に耐えられるのか＞
被締結物を2枚の圧延鋼板t6.0としましたが、これが外力により変形しないと仮定しましょう。（t6.0に10[kN]を入れたらたぶんけっこうな弾性変形を起こします。）
第３項のの検討でミーゼス応力σeq=540[MPa]までは安全という話になっていました。せん断応力τt=129[MPa]は変わらないとして、ミーゼス応力σeq=540[MPa]と置くと、その場合の引張応力は、
σf = ( σeq^2 - 3 x τt^2 )^0.5 = 492[MPa]
となります。締付けによる軸力での応力は411[MPa]でしたので、差分は81[MPa]あります。有効径の断面積をこれに積算することで、ボルトの軸力変化の許容値がわかります。
Δf(safe) = 81[MPa] x 34.2[mm^2] = 2770[N]
Qa = ΔF(safe) / ( Cb / (Cb + Cc) )
= 2770[N] / (203.67 / (203.67 + 4625.17) ) = 65674[N](6.7[tonf])
被締結物の強度を無視すると、ボルト自体は6.7トンもの外力がかかっても耐えられる計算になります。
まあ、これは単純に引張しか作用しない実験室的な状況で、被締結物の強度を無視した結果ですので、結果として緩すぎるわけですが、M8並目のボルト・ナットは被締結物との関係次第ではずいぶんと大きな荷重を伝達できることがわかります。
---------
とりあえず（その１）はこのあたりまでにします。
（その２）以降では強度区分が低い場合や被締結物の板厚、あと疲労の話などをできればなあ、とか思います。
（エターしないようがんばります。）
※参考文献
『トラブルを未然に防ぐ ねじ設計法と保全対策』
https://www.amazon.co.jp/dp/4526072583/
